Recently while reading the vector search OSS Qdrant, I learned an approach for efficient top‑k selection and took notes here.
Partial sorting
When building a search response, you often want only the top‑k items (largest values) from an array of length N.
I used to sort the whole array and slice the first k items. In Rust, that might look like:
fn top_k(v: &mut [i32], k: usize) -> &[i32] {
v.sort_by_key(|&x| std::cmp::Reverse(x));
&v[0..k]
}
fn main() {
let mut v = vec![1, 8, 2, 4, 3];
assert_eq!(top_k(&mut v, 3), vec![8, 4, 3]);
}Python and Rust use Timsort (Wikipedia), which is O(n) best‑case and O(n log n) on average/worst‑case, so the above is O(n log n).
It’s simple but wasteful when N ≫ k. With N=10,000 and k=100, there should be a more efficient method.
This is where partial sorting (Wikipedia) helps. Of several methods listed there, heap‑based algorithms are often easiest because standard libraries commonly provide BinaryHeap.
We’ll assume we want the top‑k in descending order.
BinaryHeap complexity
Costs for a binary heap:
- Peek max: O(1)
- Push: average O(1), worst O(log n)
- Pop root: average O(log n), worst O(log n)
Consider a max‑heap where the root is the maximum.
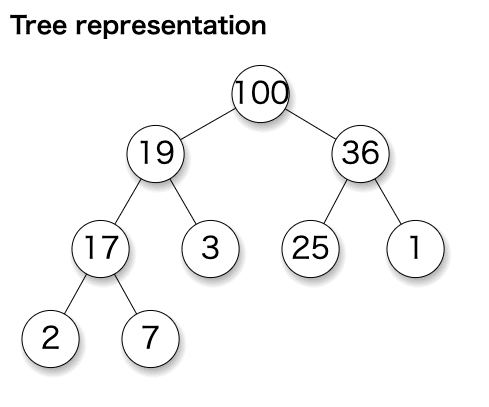
Getting the max is O(1) by looking at the root.
Why is push average O(1)? Roughly half the nodes are leaves; there’s a 50% chance insertion ends at a leaf, 25% one level up, 12.5% two levels up, etc., giving O(1)*0.5 + O(2)*0.25 + O(3)*0.125 + … = O(2).
Removing the root takes O(log n) swaps proportional to tree height.
Keep a size‑k min‑heap
Push until the heap size reaches k; once at k, on each new push, pop the root to keep size k. The heap then contains the top‑k elements.
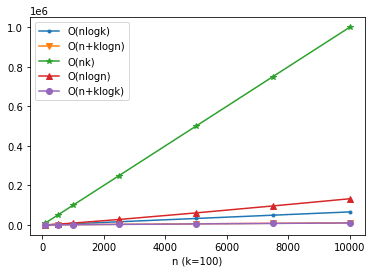
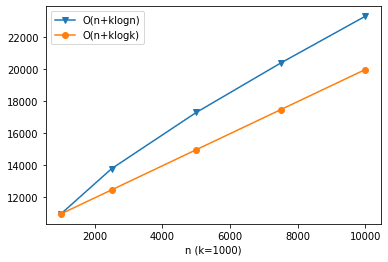
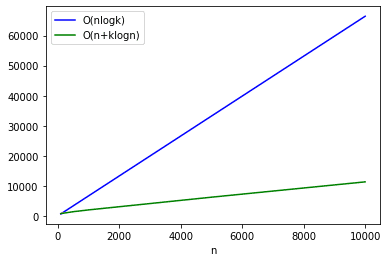
Complexity: inserting into a size‑k heap is O(log k), repeated n times → O(n log k). This keeps memory bounded at k, which helps when n is huge or data arrives online.
Qdrant uses this approach (implementation).
Build a max‑heap and pop k times
Alternatively, build a max‑heap over all n items, then pop k times to collect the top‑k in order.
This is a straightforward priority‑queue usage and may be easier to implement.
Complexity: heap construction O(n) plus k pops O(k log n), total O(n + k log n). For large n, this can beat the previous method thanks to the log n factor.
Other methods
Wikipedia’s Partial sorting lists quickselect+quicksort and mergesort+quicksort hybrids with O(n + k log k), which can be even more efficient.
Another option is bubble sort that stops after reaching the k‑th element, which is O(nk) (Wikipedia).
For reference, here are visualized complexities: