最近、Qdrantというベクトル検索のOSSを読んでいて、タイトルのやり方を知ったのでまとめておく。
部分ソート
検索のレスポンスを作るときなど、長さNの配列のうち値の高い順にk件だけソートしてほしいという時がある。
このような処理はこれまで何度も書いてきたけど、これまでは単純に配列をソートして、上位k件を切り取るという方法で実装していた。
Rustで例を作ると、高い順にk件取得する処理は、以下のような処理を書くイメージ。
fn top_k(v: &mut [i32], k: usize) -> &[i32] {
v.sort_by_key(|&x| std::cmp::Reverse(x));
&v[0..k]
}
fn main() {
let mut v = vec![1, 8, 2, 4, 3];
assert_eq!(top_k(&mut v, 3), vec![8, 4, 3]);
}
PythonやRustなどではティムソート (wikipedia) というソートアルゴリズムが利用されていて、最良でO(n)、平均と最悪は共にO(nlog(n))の計算量となる。そのため、上記のtop_kの処理はO(nlog(n))の計算量となる。
この方法は、単純であるけれど、配列の全件を並べてしまっているため、少し効率が悪くなってしまう。例えばN=10000、k=100のように全体の長さと欲しい件数に差がある場合は、より効率的な方法が存在しそうなことがイメージしやすいと思う。
このようなケースでは、部分ソート (wikipedia) と呼ばれる手法を用いると効率よく並べることができる。
wikipediaを参照すると、代表的な3つの手法が紹介されているものの、ヒープ構造を使ったアルゴリズムは、BinaryHeapが標準ライブラリで提供されることが多いので、最も簡単に実装できそう。
今回は、N件ある配列のうち、上位k件を降順に取得したいとして考えてみる。
BinaryHeapの計算量
まず、BinaryHeapの各処理における計算コストについて以下の通りになる。
- 最大値の参照：O(1)
- 要素の追加（push）: 平均O(1)、最悪O(logn)
- ルートの削除（pop）：平均O(logn)、最悪O(logn)
最大値がルートのノードとなるMaxHeapを考えてみる。
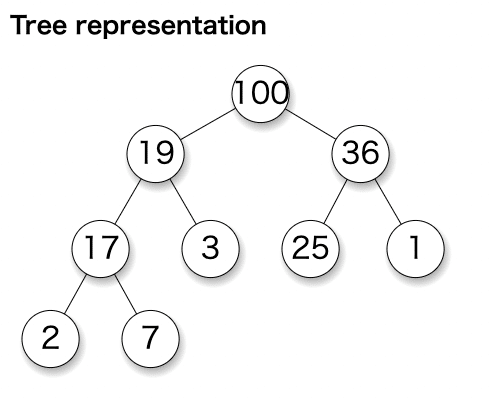
最大値を取得したい場合は常にルートを見れば良いので、最大値はO(1)となる。
追加する場合がO(1)になるのが少し直感的に分かりにくいけれど、二分木は全体の約半分は葉のノードとなるため、50%の確率で末端への追加になることに注目する。その上を辿る確率は25%、その上は12.5%、となるため、O(1) * 0.5 + O(2) * 0.25 + O(3) * 0.125 + … となり、これはO(2)となる。
ルートを削除する場合は、ツリーの高さ分だけノードを交換していく必要があるので、O (logn)となる。
k件の最小ヒープを使って値を取得する方法
ノードのサイズがk個になるまでヒープにデータをpushしていき、サイズがkに達した後はヒープに追加するたびにルートをpopすることでサイズをkに保つようにする。これにより、ヒープに含まれているノードは上位k個の要素が残ることになる。
計算量について考える。k個のノードを持つヒープを挿入コストはO(logk)で、これをn回繰り返すので全体のコストはO(nlogk)となる。これはサイズがkで固定となるため、nが大きくてメモリに乗り切らないような場合やオンラインで値を更新したい場合はよさそう。
この方法がQdrantで採用されていた。（Qdrantの実装）
最大ヒープを構築してk回値をpopする方法
こちらの方法は全件（n件）の最大ヒープを構築して、最大値をk回popする方法。popするたびに最大値が取得できるので、順に配列に追加していくと、最大値でソートされた値を取得することができる。
優先度付きキューそのままの使い方になるので、こちらの方が分かりやすいし簡単かもしれない。
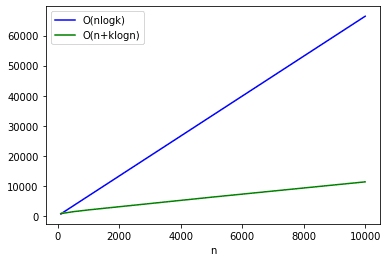
計算量はヒープの構築がO(n)で、k回のpopはO(klogn)、合計するとO(n+klogn)となる。nが大きい場合は、lognで抑えれられてる分だけ前述の方法に比べて計算量は小さくなると思う。
k=100のとき、n=100 ~ 10000の範囲での計算量
その他の方法
WikipediaのPartial sortingのページには、クイックセレクトとクイックソートを組み合わせる方法や、マージソートとクイックソートを組み合わせる方法が紹介されており、それらはO(n+klogk)となるのでより効率的になる。
他には、k個目まで要素で終了するバブルソートを使った方法もあり、その場合、O(nk)となる。（wikipediaのバブルソートのページ）
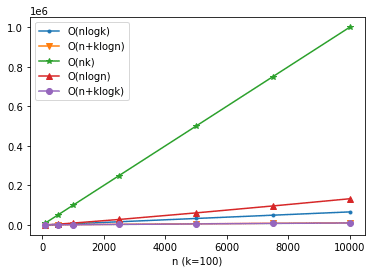
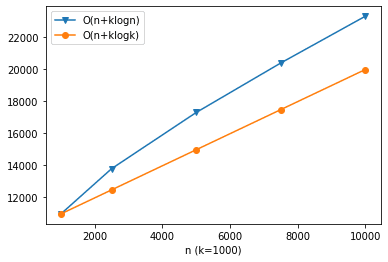
参考までに、それぞれ計算量がどれくらいになるのか可視化した。
k=100、n=100 ~ 10000で比較。O(n+klogn)とO(n+klogk)が重なって表示されている。
k=1000、n=1000 ~ 10000で比較。kが大きいと2項目の影響が大きくなるので、O(n+klogk)がより効率的であることがわかる。